B треугольнике ABC угол C = 30°, AC = 76 см, BC = 27 см. Через вершину А проведена прямая...

Ответ:

Объяснение:

Оптимальное решение задачи:

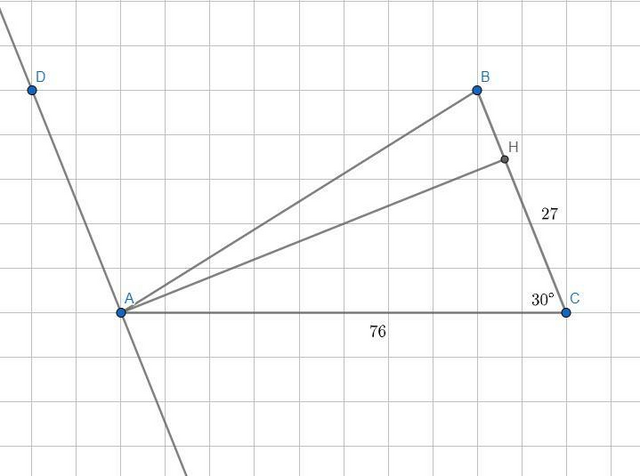
Катет против угла в 30* в прямоугольном треугольнике равен половине гипотенузы. Т.к. AH - высота, то треугольник AHC - прямоугольный. Тогда AH=76/2=38.

Приведу другое, менее оптимальное, но тоже приемлемое решение:

Найдем площадь треугольника ABC по формуле:

$S=\dfrac{1}{2}ab\times\sin\alpha$

Получим:

$S_{ABC}=\dfrac{1}{2}\times 27\times 76\times \dfrac{1}{2}=513$

Еще раз запишем формулу площади этого же треугольника, но уже по другой формуле:

$S=\dfrac{1}{2}ah$

Получим:

$AH=\dfrac{2S_{ABC}}{BC}=\dfrac{2\times513}{27}=38$