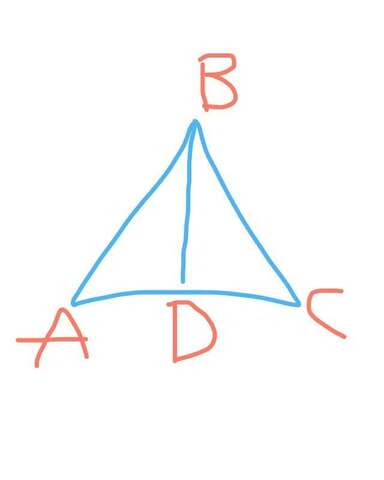
Тут получается Равнобедренный треугольник, в котором углы А и С по 30 градусов, угол АDВ и BDC по 90 и углы АВD и DBC по 60
Катет BD, являющийся высотой, лежащий напротив угла А в 30 градусов, равен половине гипотенузы AB, равной 24
Т.е. получается, что BD=24:2=12