Сторона основания правильной четырехугольной призмы равна 6 см, а диагональ боковой грани...

Question

Дано ответов: 2

maresyaaaaa23_zn · Answer 1 · 2020-06-07T05:03:04+0000

Відповідь:

Так как дана правильная призма, то в основании лежит равносторонний треугольник, а боковые грани - прямоугольники. Боковой кант равен высоте призмы. Рассматривая боковую грань, с теоремы Пифагора находишь боковой кант. Далее применяешь формулы. S(боковое)=P(переметр основания)*h. S(полное)=S(боковое)+2S(основания). И так как в основе равносторонний треугольник, то его S=(сторона умножить на корень из 3)/4. Вот краткое решение.

Покрокове пояснення:

as11111_zn · Answer 2 · 2020-06-07T05:03:04+0000

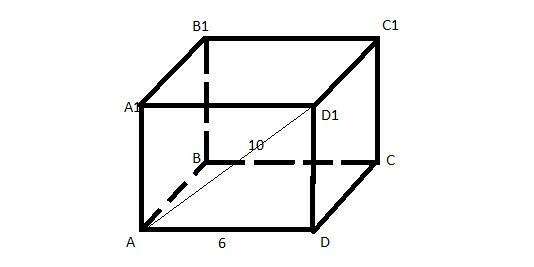
Ответ: Площадь боковой поверхности равна 192 см², а полной 264 см²

Пошаговое объяснение:

В основании правильной четырехугольной призмы лежит квадрат, а боковые стороны равные прямоугольники.

Из прямоугольного Δ $AD_{1}D$ по теореме Пифагора находим:

$D_{1}D=\sqrt{AD_{1} ^{2}-AD^{2}}=\sqrt{10^{2}-6^{2}}=8$

Площадь боковой поверхности равна:

$S_{1}=4*S_{AA_{1}D_{1}D}=4*AD*DD_{1}=4*6*8=192$

Полная поверхность равна площади боковой поверхности и площади оснований, которые являются равными квадратами:

$S=S_{1}+2*S_{ABCD}=192+2*AD^{2}=192+2*36=264$