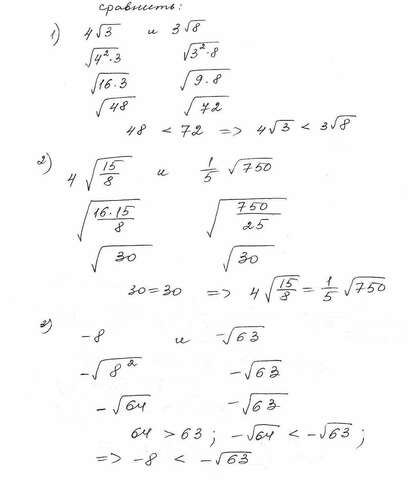\bold{4\sqrt{3} < 3\sqrt{8}} \\\\\\ 2)\\\\4\sqrt{\dfrac{15}{8} }=\sqrt{\dfrac{16\cdot15}{8} }=\sqrt{30} \\\\\dfrac{1}{5}\sqrt{750}=\sqrt{\frac{750}{25} } =\sqrt{30}\\\\30=30\ =>\bold{ 4\sqrt{\dfrac{15}{8} } =\dfrac{1}{5}\sqrt{750}} \\\\\\3)\\\\-8=-\sqrt{64} \\\\64>63;\ =>-\sqrt{64} <-\sqrt{63} \ =>\bold{-8 <-\sqrt{63}}" alt="\displaystyle\\1)\\\\ 4\sqrt{3}=\sqrt{4^2\cdot3}=\sqrt{16\cdot3} =\sqrt{48}\\\\3\sqrt{8}=\sqrt{3^2\cdot8} =\sqrt{9\cdot8}=\sqrt{72} \\\\48<72\ =>\bold{4\sqrt{3} < 3\sqrt{8}} \\\\\\ 2)\\\\4\sqrt{\dfrac{15}{8} }=\sqrt{\dfrac{16\cdot15}{8} }=\sqrt{30} \\\\\dfrac{1}{5}\sqrt{750}=\sqrt{\frac{750}{25} } =\sqrt{30}\\\\30=30\ =>\bold{ 4\sqrt{\dfrac{15}{8} } =\dfrac{1}{5}\sqrt{750}} \\\\\\3)\\\\-8=-\sqrt{64} \\\\64>63;\ =>-\sqrt{64} <-\sqrt{63} \ =>\bold{-8 <-\sqrt{63}}" align="absmiddle" class="latex-formula">
