Ответ:
S = 612см²
Объяснение:
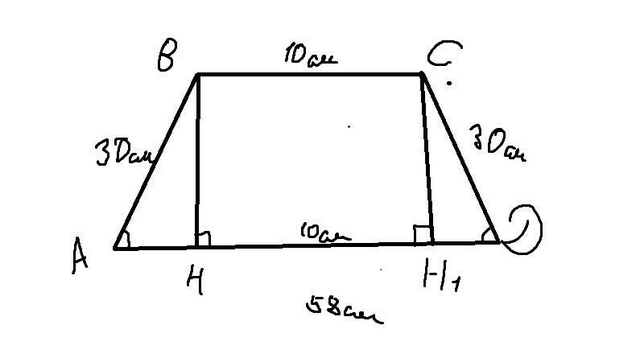
т.к. трапеция равнобедренная, то её стороны равны => P = 10+58+2x=128
2x=60
x=30см - боковая сторона. После опустим из углов два перпендикуляра BH и CH₁ => ВС = HH₁ = 10см.
Рассмотрим ABH и CH₁D они прямоугольные, AB = CD и ∠A = ∠D т.к. трапеция равнобедренная => ABH = CH₁D => AH = H₁D = 24см; С помощью теоремы пифагора находим высоту 30² - 24² = x² => x = 18см;
S = 18*( ) = 612см²
) = 612см²