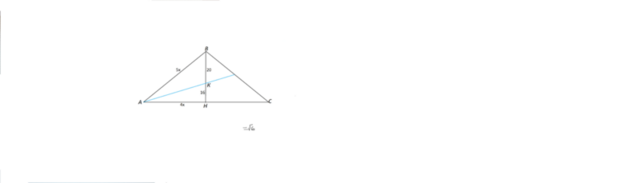
Биссектриса угла треугольника делит сторону, которую пересекает, в отношении прилежащих сторон.
Расмотрим треугольник АВН.
АН:АВ= КН:ВК=16:20=4:5
Гипотенуза и один из катетов относятся как 5:4.
Естественно предположить, что отношение всех сторон будет отношением сторон
египетского треугольника , т.е. 5:4:3
Пусть коэффициент отношения будет х
Тогда высота ВН=3х=36 см
х=12 см
АВ=5х=60 см
АН=4х=48 см
Отсюда АС=48*2=96
Р=60*2+96=216 см²
--------------
Вариант решения через т. Пифагора:
ВН²=АВ²-АН²
1296=25х²-16х²=9х²
х=12 см
АВ=60 см
АС=48*2=96 см
Р=216 см²