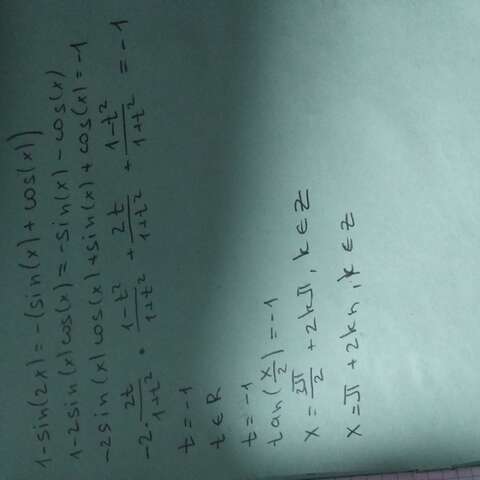Решите уравнение: 1-sin2x= -(sinx+cosx)

1 - Sin2x = - (Sinx + Cosx)

Sinx + Cosx = t , - 1 ≤ t ≤ 1

(Sinx + Cosx)² = t²

Sin²x + 2SinxCosx + Cos²x = t²

1 + Sin2x = t²

Sin2x = t² - 1

1 - (t² - 1) = - t

1 - t² + 1 = - t

t² - t - 2 = 0

t₁ = - 1

t₂ = 2 - неуд

Sinx + Cosx = - 1

Sinx + (1 + Cosx) = 0

$2Sin\frac{x}{2} Cos\frac{x}{2} +2Cos^{2}\frac{x}{2}=0\\\\2Cos\frac{x}{2}(Sin\frac{x}{2}+1)=0\\\\1)Cos\frac{x}{2}=0\\\\\frac{x}{2}=\frac{\pi }{2}+\pi n,n\in Z\\\\x=\pi+2\pi n,n\in Z\\\\2)Sin\frac{x}{2}+1=0\\\\Sin\frac{x}{2}=-1\\\\\frac{x}{2}= -\frac{\pi }{2}+2\pi n,n\in Z\\\\x=-\pi +4\pi n,n\in Z$