Ответ:
R = 2,5 см.
Объяснение:
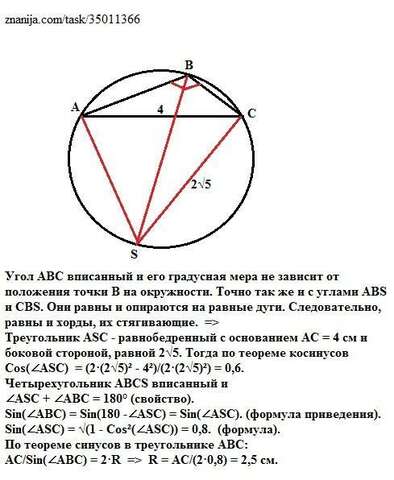
Угол АВС вписанный и его градусная мера не зависит от положения точки В на окружности. Точно так же и с углами ABS и CBS. Они равны и опираются на равные дуги. Следовательно, равны и хорды, их стягивающие. =>
Треугольник ASC - равнобедренный с основанием АС = 4 см и боковой стороной, равной 2√5. Тогда по теореме косинусов
Cos(∠ASC) = (2·(2√5)² - 4²)/(2·(2√5)²) = 0,6.
Четырехугольник АВСS вписанный и
∠ASC + ∠AВC = 180° (свойство).
Sin(∠AВC) = Sin(180 -∠ASC) = Sin(∠ASC). (формула приведения).
Sin(∠ASC) = √(1 - Сos²(∠ASC)) = 0,8. (формула).
По теореме синусов в треугольнике АВС:
АС/Sin(∠AВC) = 2·R => R = AC/(2·0,8) = 2,5 см.