Помогите пожалуйста решить номер 10

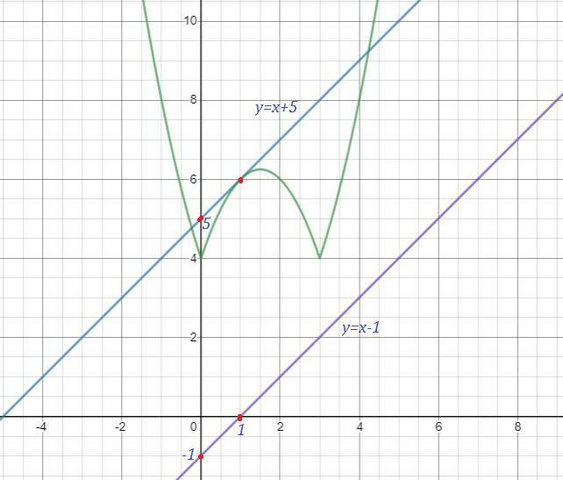
Строим график функции $y=|x^2-3x|+4$ и $y=x-1$ .

Из чертежа видно, что касательная к первому графику , параллельная у=х-1, будет единственная. Точка касания попадёт в промежуток (0,3) .

В этом промежутке заданное уравнение имеет вид $y=-x^2+3x+4$ .

Найдём угловой коэффициент касательной к вышеуказанной параболе, который совпадает с угловым коэффициентом прямой у=х-1, равный k=1

$y'=-2x+3=1\; \; \to \; \; -2x=-2\; \; ,\; \; x=1$

$y(1)=-1+3+4=6\; ,\; \; y'(1)=k=1\\\\y=y(x_0)+y'(x_0)(x-x_0)\\\\y=6+1(x-1)\\\\\boxed {\; y=x+5\; }$