#1.
Чтобы узнать, принадлежит ли графику функции точка, нужно подставить значение точки под x , и проверить, будет ли значение на оси y таким же:
a) A (-2;6)
(-2)² + 2 = 4 + 2 = 6 - верно ⇒ A принадлежит графику функции y = x² + 2
б) B (0; 2)
0² + 2 = 2 - верно ⇒ B принадлежит графику функции y = x² + 2
в) C (-1;1)
(-1)² + 2 = 1 + 2 = 3 - неверно ⇒ C принадлежит графику функции y = x² + 2
#2.
y = x³ - 9
Чтобы узнать точки пересечения с осями, нужно переменные приравнять к нулю:
y = 0 ⇒ x³ - 9 = 0
x³ = 9
x = ∛9 - точка пересечения графика функции с осью Y.
x = 0 ⇒ y = 0 - 9
y = -9 - точка пересечения графика с осью X
#3.
Линейной называют функцию типа y = kx+b
a) y = 8 - 7x - эта функция типа y = kx+b ⇒ y = 8 - 7x - линейная, k = -7; b = 8;
б) y = 2x² + 4 - это квадратичная функция ⇒ не линейная
в) 
- это функция типа y = kx+b ⇒ - линейная, k = 
; b = 0;
г) y = -4 - это функция типа y = kx+b ⇒ y = -4 - линейная, k = 0; b = -4.
#4.
a) Если x = -3, то 
б) Если 
, то 
x = \frac{1}{3} * \frac{3}{1} = 1" alt="\frac{1}{3} = \frac{1}{3} x => x = \frac{1}{3} * \frac{3}{1} = 1" align="absmiddle" class="latex-formula">
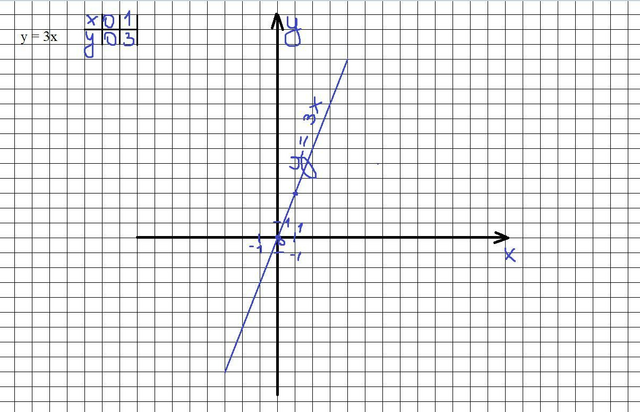
#5.
График на фотографии
(Берем две точки:
1) x = 0 ⇒ y = 0
2) x = 1 ⇒ y = 3)
