Это сложно объяснить, но ответ получился 12... Надеюсь, это верный ответ)
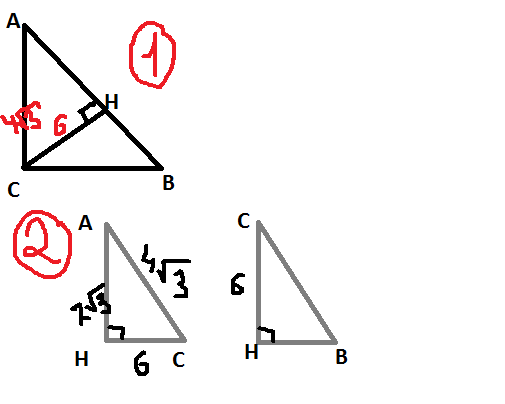
Итак, вот рисунок, по задаче, чтобы было понятнее о чем я говорю)
1) Рассмотрим треугольник АСВ, смотрим и видим, что треугольник АНС прямоугольный, так как СН-высота... тогда по т. Пифогра найдем АН...
Надеюсь формулу знаете...
Получаем, что АН=2
2) Но треугольники АНС И НСВ подобные( по первому признаку подобия треугольников), а значит составляем пропорцию:
 =
=  (2 рисунок)
(2 рисунок)
а далее подставляем числа..
 =
= 
Отсюда получаем


Корни сократятся, а 24 и 2 сокращаем на 2 и получаем ответ 12))
х=12, т.е. ВС=12