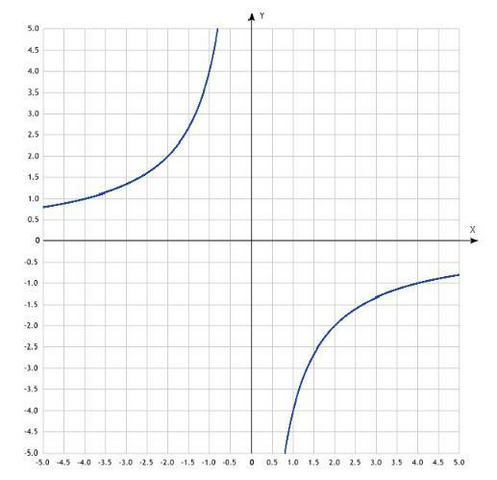
1.На рисунке изображён график функции y=kx. По данному графику определи значение k.
2.Дана арифметическая прогрессия: 19; 23; 27... Найди сумму её первых семнадцати членов.
3.объём цилиндра вычисляется по формуле V=π⋅R2⋅h, где V — объём, h — высота цилиндра. Пользуясь этой формулой, определи значение h, если V=20⋅π, R=5. (Ответ округли до тысячных).
4.Укажи, при каких значениях b значение выражения 21⋅b+12 меньше значение выражения 20⋅b−4? В ответе укажи номер правильного варианта.
1) b>12;
2) b<12;
3) b<−16;
4) b>−16.
5.Какое число спиц содержит колесо, у которого угол между любыми двумя соседними спицами равен 24 градусов?
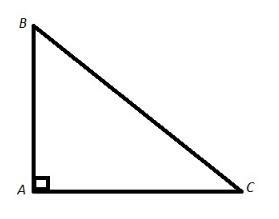
6.Известно, что в прямоугольном треугольнике ABC с прямым углом A гипотенуза BC=10, sinC=0,4. Определи длину катета AB.
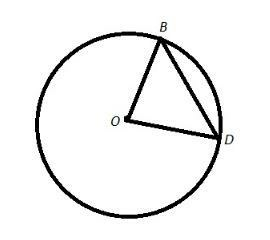
7.Дуга BD окружности равна 60°. Радиус окружности равен 15. Найди длину хорды BD
8.Известно, что стороны прямоугольника относятся как 2:21, площадь прямоугольника равна 378. Найди периметр данного прямоугольника.
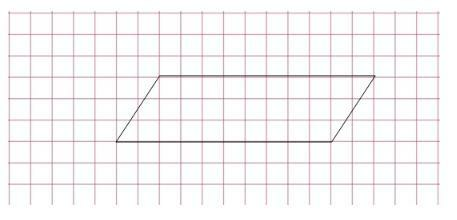
9.На рисунке изображён параллелограмм. Найди его площадь (клетка имеет размер 1 на 1).
10.Выбери верное утверждение. В ответе укажи его номер.
1. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
2. Вписанные углы, опирающиеся на одну и ту же дугу, имеют разные градусные меры.
3. Если при пересечении двух прямых секущей сумма односторонних углов равна 360 градусов, то прямые параллельны.