Построить график функции и записать ее свойства: y=3x^5-5x^3

Question

Дан 1 ответ

nikebod313_zn · Answer 1 · 2020-06-08T08:03:05+0000

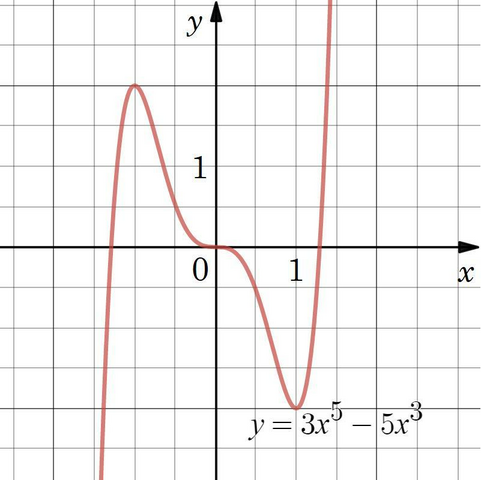
Задана функция $f(x) = 3x^{5} - 5x^{3}$

1) Найдем область определения функции:

$D(f) = (-\infty; \ +\infty)$ , то есть $x \in \mathbb{R}$

2) Исследуем функцию на четность:

$f(-x) = 3(-x)^{5} - 5(-x)^{3} = -3x^{5} + 5x^{3} = -(3x^{5} - 5x^{3}) = -f(x)$

Функция нечетная, непериодическая.

3) Найдем точки пересечения графика функции с осями координат:

Если $x = 0$ , то $y = 0$ , значит $(0; \ 0)$ — точка пересечения с осью $Oy$ .

Если $y = 0$ , то есть $3x^{5} - 5x^{3} = 0$ , то:

$x^{3}(3x^{2} - 5) = 0$

$\left[\begin{array}{ccc}x^{3} = 0 \ \ \ \ \ \ \ \\3x^{2} - 5 = 0\\\end{array}\right$

$\left[\begin{array}{ccc}x = 0 \ \ \ \ \ \ \ \\ x = \pm \dfrac{\sqrt{15}}{3} \\\end{array}\right$

Значит $(0; \ 0)$ , $\left(-\dfrac{\sqrt{15}}{3}; \ 0 \right)$ и $\left(\dfrac{\sqrt{15}}{3}; \ 0 \right)$ — точки пересечения с осью $Ox$ .

4) Асимптот данная функция не имеет, поскольку она непрерывная на всей области определения.

5) Найдем производную и критические (стационарные) точки функции:

$f'(x) = (3x^{5} - 5x^{3})'= 15x^{4} - 15x^{2}$

Из уравнения $15x^{4} - 15x^{2} = 0$ имеем критические точки:

$x_{1} = -1; \ x_{2} = 0; \ x_{3} = 1$

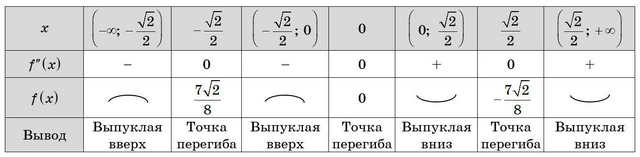
6) Найдем промежутки возрастания, убывания и экстремумы функции, заполнив таблицу (см. вложение).

7) Исследуем функцию на выпуклость и точки перегиба с помощью второй производной:

$f''(x) = (15x^{4} - 15x^{2})' = 60x^{3} - 30x$

Если на промежутке $(a; \ b)$ дифференцируемая функция $f(x)$ имеет положительную вторую производную, то есть 0" alt="f''(x) > 0" align="absmiddle" class="latex-formula"> для всех $x \in (a; \ b)$ , то график этой функции на $(a; \ b)$ является выпуклым вниз; если на промежутке $(a; \ b)$ дифференцируемая функция $f(x)$ имеет отрицательную вторую производную, то есть $f''(x) < 0$ для всех $x \in (a; \ b)$ , то график этой функции на $(a; \ b)$ является выпуклым вверх.