Відповідь:
1620 см²
Пояснення:
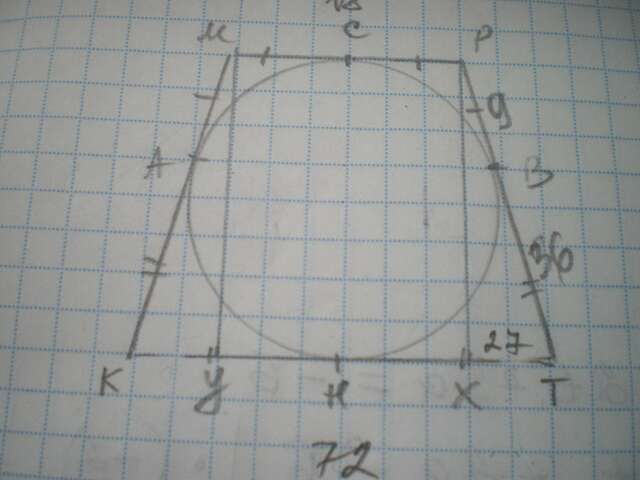
Дано: КМРТ - трапеція, АМ=РВ=9 см, АК=ВТ=36 см. Знайти S(КМРТ).
За властивістю дотичної до кола, відрізки дотичних проведені до кола з однієї точки, рівні.
Трапеція рівнобедрена за умовою, тому АМ=МС=СР=РВ=9 см;
АК=КН=НТ=ВТ=36 см.
Отже МР=9+9=18 см; КТ=36+36=72 см.
Проведемо висоти МУ та РХ, ХУ=МР=18 см, КУ=ТХ=(72-18):2=27 см.
Розглянемо ΔРТХ - прямокутний, РТ=9+36=45 см.
За теоремою Піфагора РХ=√(РТ²-ТХ²)=√(2025-729)=√1296=36 см.
S(СКМТ)=(18+72):2*36=15*12=1620 см²