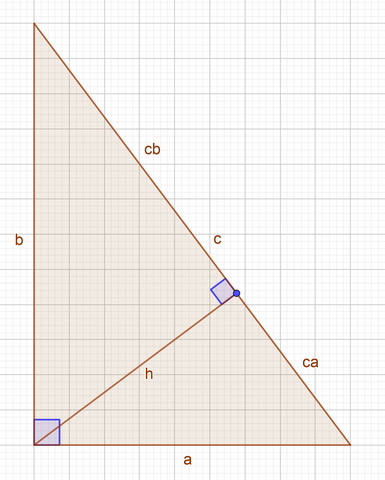
Обозначим катеты за a = 9 см, b = 12 см , гипотенузу за c, высоту за h, проекции катетов на гипотенузу за ca и ba.
Исходя из т. Пифагора, следует:
 c=\sqrt{a^2+b^2} \\c = \sqrt{9^2+12^2}= \sqrt{81+144} = \sqrt{225} = 15 \:\: (cm)" alt="c^2=a^2+b^2 => c=\sqrt{a^2+b^2} \\c = \sqrt{9^2+12^2}= \sqrt{81+144} = \sqrt{225} = 15 \:\: (cm)" align="absmiddle" class="latex-formula">
c=\sqrt{a^2+b^2} \\c = \sqrt{9^2+12^2}= \sqrt{81+144} = \sqrt{225} = 15 \:\: (cm)" alt="c^2=a^2+b^2 => c=\sqrt{a^2+b^2} \\c = \sqrt{9^2+12^2}= \sqrt{81+144} = \sqrt{225} = 15 \:\: (cm)" align="absmiddle" class="latex-formula">
Найдет площадь прямоугольного треугольника:

Воспользуемся формулой площади треугольника через высоту и выразим из нее высоту:
 2S = h\cdot c_h => h = \frac{2S}{c_h} \\h = \frac{2\cdot 54}{15} = \frac{108}{15}= 7\frac{3}{15} =7\frac{1}{5}=7,2 \:\: (cm)" alt="S = \frac{h\cdot c_h}{2} => 2S = h\cdot c_h => h = \frac{2S}{c_h} \\h = \frac{2\cdot 54}{15} = \frac{108}{15}= 7\frac{3}{15} =7\frac{1}{5}=7,2 \:\: (cm)" align="absmiddle" class="latex-formula">
2S = h\cdot c_h => h = \frac{2S}{c_h} \\h = \frac{2\cdot 54}{15} = \frac{108}{15}= 7\frac{3}{15} =7\frac{1}{5}=7,2 \:\: (cm)" alt="S = \frac{h\cdot c_h}{2} => 2S = h\cdot c_h => h = \frac{2S}{c_h} \\h = \frac{2\cdot 54}{15} = \frac{108}{15}= 7\frac{3}{15} =7\frac{1}{5}=7,2 \:\: (cm)" align="absmiddle" class="latex-formula">
Проекции катетов будут равны:

или 
—————————————————————————————
Высоту и проекции катетов также можно найти через пропорциональные отрезки в прямоугольном треугольнике:
– высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:
 h=\sqrt{ca\cdot cb}" alt="h^2 = ca\cdot cb => h=\sqrt{ca\cdot cb}" align="absmiddle" class="latex-formula">
h=\sqrt{ca\cdot cb}" alt="h^2 = ca\cdot cb => h=\sqrt{ca\cdot cb}" align="absmiddle" class="latex-formula">
– катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:
 ca = \frac{a^2}{c} \\b^2 = cb\cdot c = > cb = \frac{b^2}{c}\\\\" alt="a^2 = ca\cdot c = > ca = \frac{a^2}{c} \\b^2 = cb\cdot c = > cb = \frac{b^2}{c}\\\\" align="absmiddle" class="latex-formula">
ca = \frac{a^2}{c} \\b^2 = cb\cdot c = > cb = \frac{b^2}{c}\\\\" alt="a^2 = ca\cdot c = > ca = \frac{a^2}{c} \\b^2 = cb\cdot c = > cb = \frac{b^2}{c}\\\\" align="absmiddle" class="latex-formula">
—————————————————————————————

Ответ: гипотенуза равна 15 см, высота — 7,2 см, проекции катетов — 5,4 см и 9,6 см.