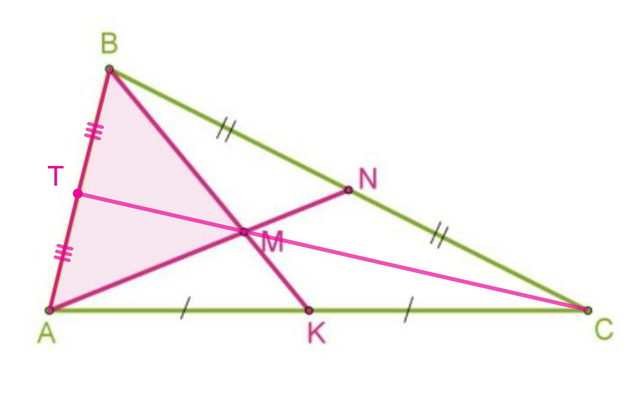
Задача: В треугольнике ABC проведенные медианы AN и BK пересекаются в точке M. Определить площадь треугольника ABC, если площадь треугольника ABM равна 10 см².
Решение:
- Медианы пересекаются в одной точке.
- Медиана разбивает треугольник на 2 треугольника одинаковой площади
- Весь треугольник разделяется своими медианами на 6 равновеликих треугольников.
Проводив третью медиану CT через т. М.
MT — медиана ΔAMB, делит ΔAMB на два треугольника одинаковой площади:


Ответ: Площадь ΔABC = 30 см².