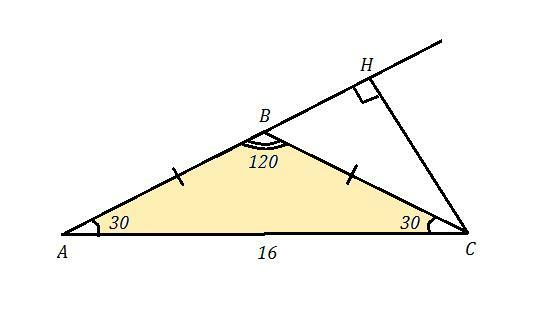
ΔАВС , ∠В=120° , АВ=ВС , АС=16 см , СН⊥АВ . Найти: СН .
Так как ΔАВС равнобедренный, АВ=ВС, то углы при его основании равны между собой: ∠ВАС=∠ВСА=(180°-120°):2=30°.
Так как треугольник тупоугольный, то основание высоты СН , точка Н , попадёт на продолжение стороны АВ. Получим прямоугольный треугольник АСН , у которого ∠НАС=∠ВАС=30°.
∠НСА=90°-30°=60°
Катет СН лежит против угла в 30°, значит он равен половине гипотенузы АС, то есть СН=1/2*АС=1/2*16=8 (см) .
Ответ: высота СН=8 см .