Изобразите ** комплексной плоскости множество точек z, удовлетворяющих условию 2 < |z| < 3

Question 1

Изобразите на комплексной плоскости множество точек z, удовлетворяющих условию 2 < |z| < 3

Question 2

$2 < |z| < 3$

Распишем модуль:

$2 < \sqrt{x^2+y^2} < 3$

$2^2 <x^2+y^2 < 3^2$

Уравнения $x^2+y^2=2^2$ и $x^2+y^2=3^2$ - уравнения окружности.

Неравенство 2^2" alt="x^2+y^2 >2^2" align="absmiddle" class="latex-formula"> определяет часть плоскости вне окружности с радиусом 2.

Неравенство $x^2+y^2 <3^2$ определяет часть плоскости внутри окружности с радиусом 3.

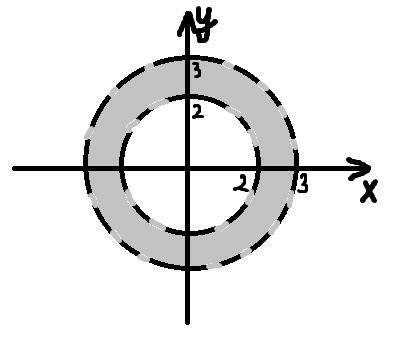
Значит, неравенство $2^2 <x^2+y^2 < 3^2$ определяет кольцо, ограниченное окружностями с радиусами 2 и 3.

Artem112_zn · Answer 1 · 2020-06-08T15:41:08+0000