Ответ:
Пошаговое объяснение:
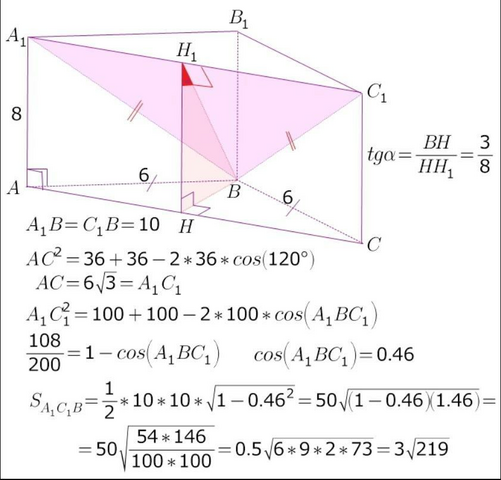
плоскость сечения можно найти, вычислив плоскость основания...
Площадь ортогональной проекции многоугольника на плоскость
= площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций)))
в нашем случае проектируемый многоугольник --это сечение)))
следовательно, его площадь будет = Sоснования / cos(HBH₁)
Sсечения = 18*sin(120°) * BH₁ / 3 = 3√3 * √(100-27) = 3√219
я это же нашла по т.косинусов)))