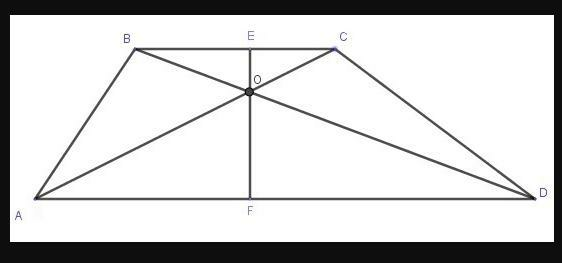
Ответ:
EO и OF - являются расстояниями от точки пересечения диагоналей до основания BC и AD, соответственно. ЕО - высота треугольника BOC и OF - высота треугольника AOD.
∠BCA = ∠CAD как накрест лежащие при BC || AD и секущей AC
∠BOC = ∠AOD как вертикальные
Следовательно, ΔBOC ~ ΔAOD (по двум углам).
Соответствующие высоты подобных треугольников относятся как соответствующие стороны, их коэффициент подобия есть отношение расстояний k = OF/OE =6/2=3
Пусть BC = x см, тогда AD = 3x см. Из условия BC + AD = 36
x + 3x = 36
4x = 36
x = 9 см.
Итак, основания трапеции 9 см и 3*9 = 27 см.
Объяснение: