1. Пусть задана окружность с центром в точке  и радиусом
и радиусом  . Из точки
. Из точки  , лежащей вне окружности, проведены две касательные
, лежащей вне окружности, проведены две касательные  и
и  , равные между собой по свойству касательных, проведенных из данной точки к окружности. Здесь
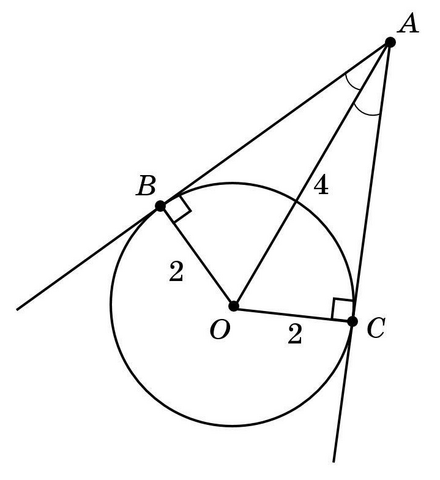
, равные между собой по свойству касательных, проведенных из данной точки к окружности. Здесь  (см. вложение).
(см. вложение).
Радиусы, проведенные из центра окружности к касательным, перпендикулярны касательным.
Имеем два равных прямоугольных треугольника  и
и  , катеты которых
, катеты которых  и
и  соответственно равны половине гипотенузы
соответственно равны половине гипотенузы  .
.
Катет прямоугольного треугольника, лежащий против угла в  , равен половине гипотенузы. Следовательно,
, равен половине гипотенузы. Следовательно, 
Тогда 
Таким образом, 
Ответ: 120°
2. Пусть задан треугольник  , в который вписана окружность с точками касания
, в который вписана окружность с точками касания  соответственно на сторонах
соответственно на сторонах  . Известно:
. Известно:  (см. вложение).
(см. вложение).
Отрезки  и
и  можно рассматривать как касательные, проведенные из точки
можно рассматривать как касательные, проведенные из точки  . Отрезки касательных, проведенных из одной точки, равны, поэтому
. Отрезки касательных, проведенных из одной точки, равны, поэтому 
Аналогично:  и
и 
Тогда:



Периметр треугольника  :
:

Ответ: 34.