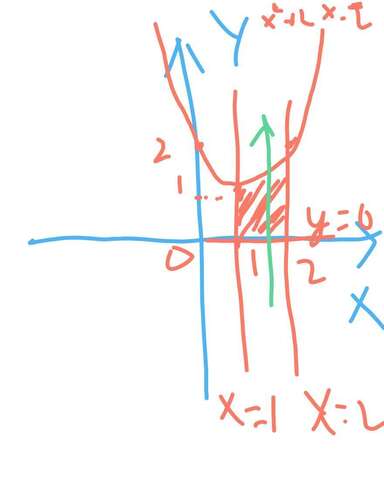
(За кривой рисунок извини, как смог)
Строим график. Из него берём пределы интегрирования по x {1≤x≤2} и по y {0≤y≤x^2+2x-2} ( предел интегрирования по у определяем по зелёной линии где входит и где выходит)
S=∫∫f(x)d(x)d(y) (по области D) = ∫(от 1 до 2)d(x)∫(от 0 до x^2-2x+2)d(y) = ∫(от 1 до 2) (x^2-2x+2) d(x) = ∫(от 1 до 2) x^2 d(x) - ∫(от 1 до 2) 2x d(x) + ∫(от 1 до 2) 2 d(x) = x^3/3 | (от 1 до 2) - x^2 | (от 1 до 2) + 2x | (от 1 до 2) = 8/3 -1/3 - ( 2-1/2) + (4-2) = 7/3 - 3/2 +2 = 5/6+2 = 17/6