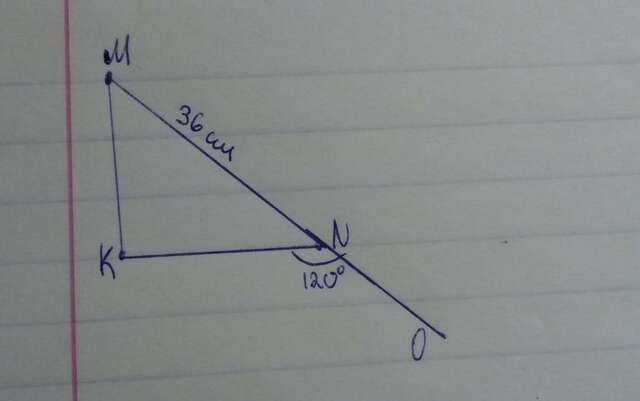
1. Т.к. в условии есть речь о гипотенузе и катете, то △MKN — прямоугольный. Обозначим за прямой угол MKN (или же просто K). Он равен 90°.
Обозначим внешний угол к вершине N — «KNO» и найдем угол MKN, смежный с ним. Для этого применим теорему: «сумма смежных углов равна 180 градусов»
∠MKN = 180°−120° = 60°
2. Теперь мы можем найти ∠KMN, т.к. нам известны два угла в треугольнике MKN, и то, что общая сумма всех трёх углов равна 180 градусов.
∠KMN = 180°−(90°+60°) = 30°.
(Можно также найти ∠KMN просто отняв от 90-ста градусов 60 градусов, применяя первое свойство прямоугольных треугольников: «сумма двух острых углов прямоугольного треугольника равна 90°»
)
3. Теперь, зная чему равны все углы треугольника и гипотенуза MN, мы можем найти катет KN, применяя 2-е свойство прямоугольных треугольников: «катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы»
То есть KN = ¹/₂MN.
KN = 36 ÷ 2 = 18.
Ответ: KN = 18 см.