Ответ:
Доказательство в объяснении и приложении.
Объяснение:
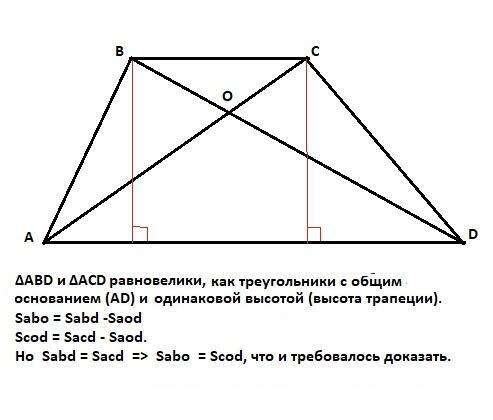
ΔABD и ΔАСD равновелики, то есть площади этих треугольников равны (Sabd = Sacd),так как эти треугольники с общим основанием (AD) и одинаковой высотой (высота трапеции). С другой стороны, площади этих треугольников равны разности:
Sabo = Sabd -Saod
Scod = Sacd - Saod.
Но Sabd = Sacd =>
Sabo = Scod, что и требовалось доказать.