Знайти площу прямокутного трикутника в якому висота, опущена із вершини прямого кута на...

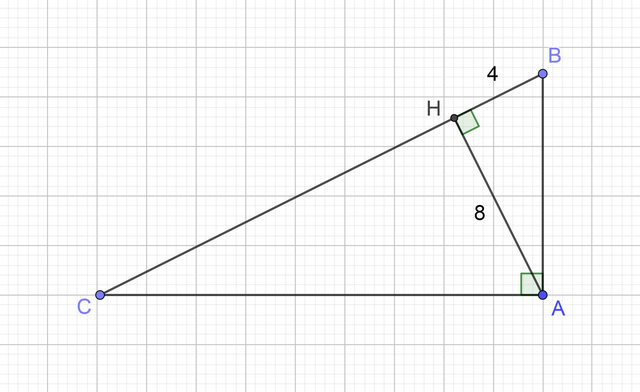
Задача: Найти площадь прямоугольного треугольника, в котором высота, опущенная из вершины прямого угла на гипотенузу, равна 8 см, и одна из проекций катета на гипотенузу равна 4 см.

Решение:

Дан ΔABC, ∠C = 90°, CH = 8 см — высота, AH = 4 см — проекция катета AC.

Из определения, высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.

$CH^2=AH\cdot BH \:\: \Rightarrow \:\: BH = \frac{CH^2}{AH} \\\\BH = \frac{8^2}{4} =\frac{64}{4}= \frac{16\cdot 4}{4} = 16 \:\: (cm)$

Тогда длина гипотенузы будет равна:

$AB = AH+BH\\AB = 4+16= 20 \:\: (cm)$

Подставим значения в формулу площади треугольника:

$S = \frac{1}{2} a\cdot h_a=\frac{1}{2} AB\cdot CH\\\\S = \frac{20\cdot 8}{2} = 10\cdot 8 = 80 \:\: (cm^2)$

Ответ: Площадь треугольника равна 80 см².

Знайти площу прямокутного трикутника в якому висота, опущена із вершини прямого кута **...