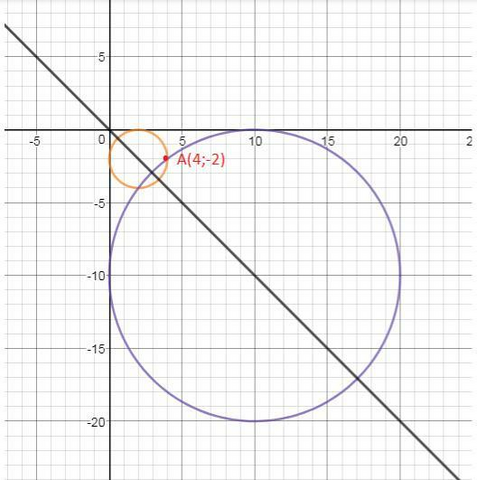
Ответ:
Окружность касается осей координат и проходит через точку, расположенную в четвертой координатной четверти, значит центр окружности лежит на биссектрисе второго и четвертого координатных углов, т.е на прямой y = – x.
и потому центр окружности имеет координаты (R;–R)
Следовательно, уравнение окружности имеет вид
(x – R)2 + (y –(– R))2 = R2.
Поскольку точка A(4;–2) лежит на окружности, координаты этой точки удовлетворяют полученному уравнению,
т.е.
(4 – R)2 + (–2 + R)2 = R2.
16–8R+R2+4–4R+R2=R2
R2–12R + 20 = 0
D = 144–80 = 64
R = 2 или R = 10
(x - 2) 2 + (y + 2) 2 = 4 или
(x - 10) 2 + (y + 10) 2 = 100
.
Объяснение: