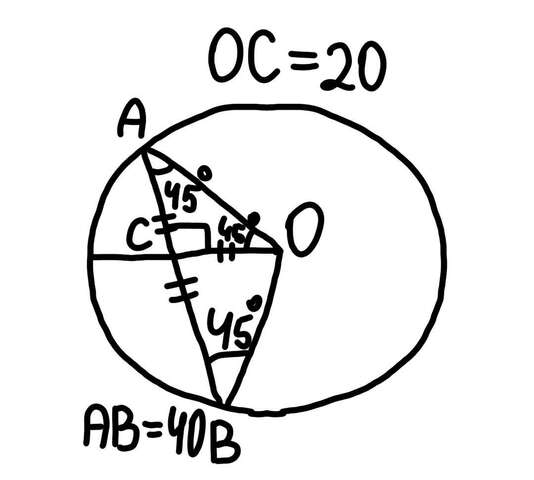
Дано: окр. с центром m0, хорда АВ, радиус ОС, ей перпендикулярный. ОС = 20см. Угол ОАВ = 45°.
Найти: АВ.
Решение:
Если АО и ОВ - радиусы, то треугольник ВАО р/б, медиана, проведённая к основанию, является биссектрисой и высотой.
Значит, треугольник АСО прямоугольный равнобедренный, унлы при основании равны, их сумма 90°. Соответственно, ОС=АС=СВ=20см. АВ=20+20=40см.
Ответ: 40см.