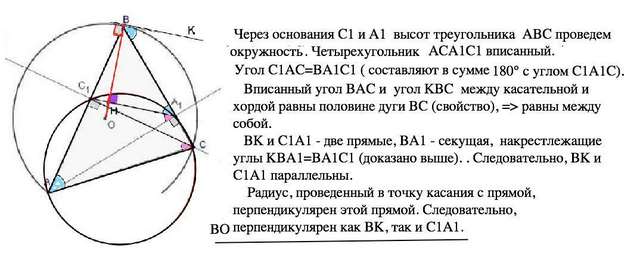
Отрезок, соединяющий основания высот треугольника, является стороной ортотреугольника (т.е. треугольника, вершинами которого являются основания высот исходного). Радиусы описанной окружности, проведённые к вершинам треугольника, перпендикулярны соответствующим сторонам ортотреугольника.
Доказательсто: У прямоугольных треугольников АС1С и АА1С общая гипотенуза, а, значит, около них можно описать одну окружность. Четырехугольник АСА1С1 вписанный. Сумма противоположных углов вписанного четырехугольника 180°.
Угол С1АС=угол ВА1С1 ( составляют 180° в сумме с углом С1А1С)
Вписанный угол ВАС и угол ВАС - между касательной и хордой – равны половине дуги ВС ( свойство), следовательно, ∠ВАС=∠ВАС
Прямые ВК и С1А1 пересекаются секущей ВА1, накрестлежащие ∠КВА1=∠ВА1С1 ( доказано выше).⇒ ВК и С1А1 параллельны.
Радиус, проведенный в точку касания с прямой, перпендикулярен этой прямой. Следовательно, ВО перпендикулярен как ВК, так и С1А1, что и требовалось доказать.