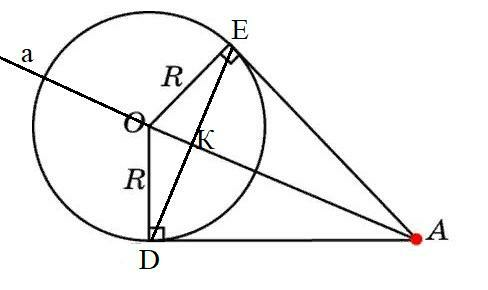
В круге с центром О, провели хорду DE, которая не проходит через точку О. Через точку О проведена прямая которая перпендикулярна к хорде DE. Докажите, что точка пересечения касательных к окружности, проведенных через точки D и E, принадлежит этой прямой.
Объяснение:
а⊥DE, АD и АЕ касательные.
Доказать А∈а
Доказательство.
ΔАЕО=ΔАDO как прямоугольные по катету и гипотенузе ( ∠АЕО=∠АDО=90° по свойству касательной ,ОЕ=ОD как радиусы, АО-общая ). В равных треугольниках соответственные элементы равны :∠ЕОА=∠DОА.
ΔЕОА=ΔDОА по двум сторонам и углу между ними :ОЕ=ОD как радиусы, ОК-общая , ∠ЕОА=∠DОА ( см выше).В равных треугольниках соответственные элементы равны ⇒∠ОКD=∠ОКЕ и этиже углы в сумме дают 180°, как смежные, т.е.∠ОКD=∠ОКЕ=90°. Значит отрезок ОА⊥DЕ. Через точку О , не лежащую на данной прямой DЕ можно провести только одну прямую перпендикулярную данной. Значит а и ОА совпадают ⇒А∈а