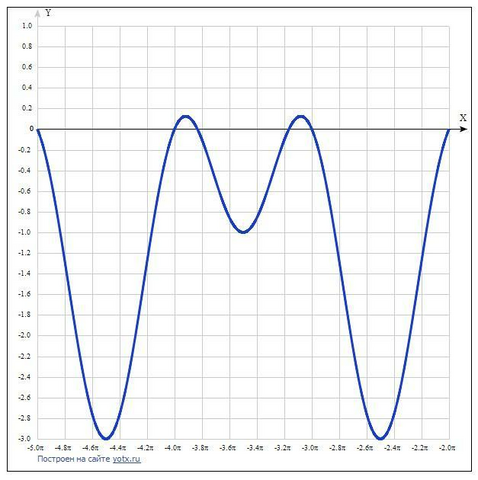
Основание в нулевой степени - это 1.
Значит, 2 - cos(2x) - sin(x) = 1, или cos(2x) + sin(x) = 1.
Заменим cos(2x): 1 - 2sin²(x) + sin(x) = 1,
sin(x)(1 - 2sin(x)) = 0.
Первый множитель имеет 1 решение:
x = πn, n ∈ Z.
Второй имеет 2 решения:
(1 - 2sin(x)) = 0,
sin(x) = 1/2.
x = 2πn + (π/6), n ∈ Z.
x = 2πn + (5π/6), n ∈ Z.
Заданному отрезку принадлежит 4 корня:
x = -3π, x = -4π.
n = -2, x = -4π + (π/6) =(-23/6)π,
n = -2, x = -4π + (5π/6) =(-19/6)π.