Ответ:
26 см.
Объяснение:
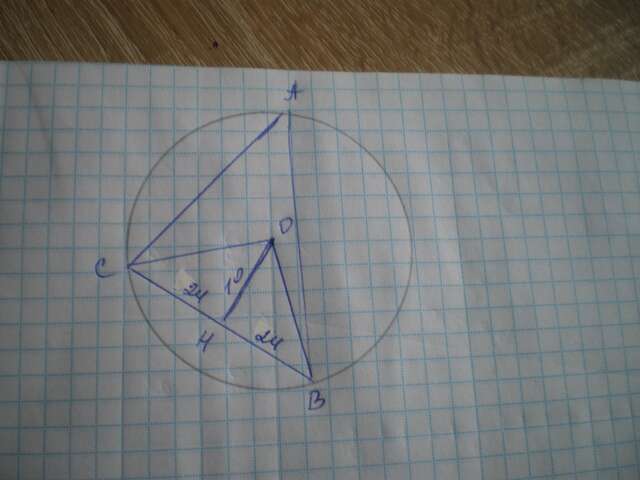
Имеем ΔСОВ - равнобедренный, т.к. он образован радиусами окружности; ОН - высота, т.к. ОН⊥ВС; ОН - медиана, т.к. ΔСОВ равнобедренный; СН=ВН=48:2=24 см.
Найдем СО из ΔСОН по теореме Пифагора:
СО=√(СН²+ОН²)=√(576+100)=√676=26 см.