Ответ:
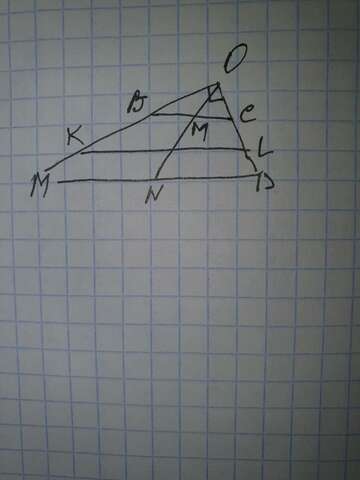
Пусть ABCD — данная трапеция, AD — большее основание, K и L — середины сторон AB и CD соответственно.
Сумма углов при одном из оснований равна (50° + 40°) = 90°, так что это большее основание AD.
∠AOD = 180° − (50° + 40°) = 90°.
По теореме: если сумма углов при основании трапеции равна 90 градусов, то длина отрезка, соединяющего середины оснований, равна полуразности длин оснований.
Пусть N — середина основания AD. Тогда ON =медиана прямоугольного треугольника AOD.
Поскольку медиана ON делит пополам любой отрезок с концами на сторонах AO и DO треугольника AOD и параллельный стороне AD, она пересекает основание BC также в его середине M.
OM=BC/2 -> MN=AD-BC/2.
Средняя линия KL при этом равна AD+BC/2
Получаем, что AD=MN+KL=6+2=8; BC=KL-MN=6-2=4.
Объяснение:
Ответ: 8; 4.