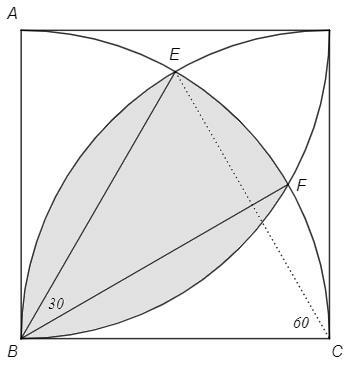
Примем сторону квадрата 1.
Точки искомой площади удалены от трех вершин не более радиуса. То есть расположены в каждом из трех секторов. Ищем их пересечение.
Треугольник BCE равносторонний => BCE=EBC=60, ABE=EBF=FBC=30
Искомая фигура состоит из сектора 30° и двух сегментов 60°.
Площадь единичного круга равна п
Площадь сектора 30 = п/12
Площадь сегмента 60 = п/6 - √3/4
S= п/12 +2(п/6 -√3/4) =5/12 п -√3/2 ~0,4429