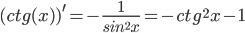y=ctg(x^2+1)·sin6x
Решение:
(sin(6x)·ctg(x^2+1))' = (ctg(x^2+1))'·sin(6x)+ctg(x^2+1)·(sin(6x))' = 2·x·(-ctg(x^2+1)2-1)·sin(6x)+ctg(x^2+1)·6·cos(6x)
Здесь:
(ctg(x^2+1))' = 2x·(-ctg(x^2+1)2-1)
(sin(6x))' = (sin(6x))'(6x)' = 6·cos(6x)
(6x)' = 6
Ответ:
2·x·(-ctg(x^2+1)2-1)·sin(6x)+6·cos(6x)·ctg(x^2+1)
При вычислении были использованы следующие правила дифференцирования:
(xa)' = axa-1
(a)' = 0
(uv)' = u'v + uv'
(f(g(x)))' = f(x)'*g(x)'