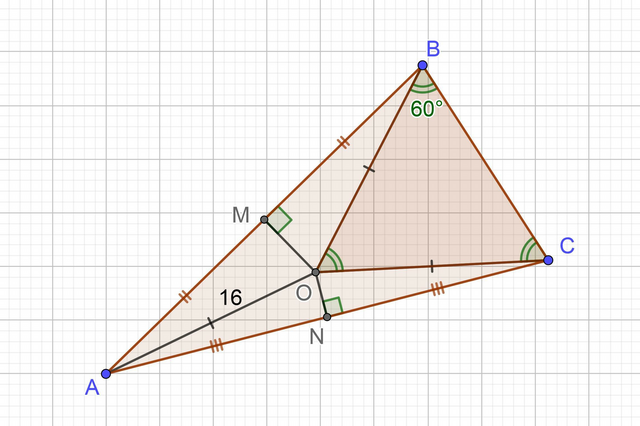
Решение:
ΔAOC — равнобедренный с основой АС, т.к. ON — высота и медиана (AN = CN) треугольника ⇒ AO = CO = 16.
ΔAOB — равнобедренный с основой AB, т.к. OM — высота и медиана (AM = CM) треугольника ⇒ AO = BO = 16.
ΔOBC — равнобедренный с основой BC, т.к. BO = CO = 16.
Тогда ∠OBC = ∠OCB = 60°,
следовательно, ∠BOC = 180−60−60 = 60° ⇒ ΔOBC — равносторонний:
BO = CO = BC = a = 16
Подставим значение в формулу площади правильного треугольника:
(квадратных единиц)
Ответ: Площадь ΔOBC равна 64√3 кв. ед.
