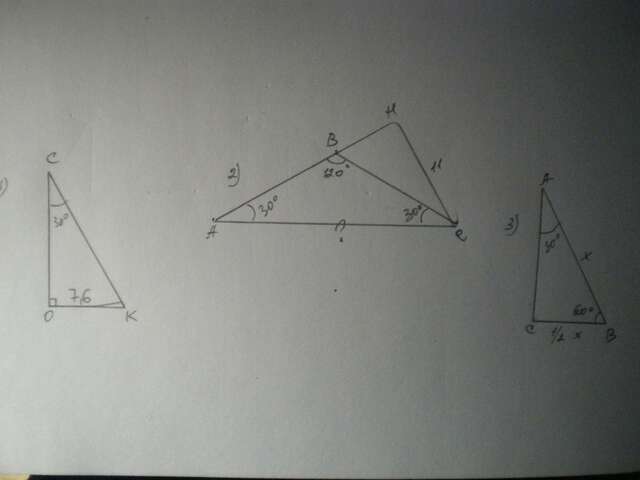
1.
Катет, лежащий против угла 30°, равен половине гипотенузы.
СК=2ОК=7,6*2=15,2 см.
2.
∠ВАС=∠ВСА как углы при основании равнобедренного треугольника, ∠ВАС=∠ВСА=(180-120):2=30°.
Проведем высоту СН=11 см (она упадет на продолжение стороны АВ)
ΔАВН - прямоугольный, ∠А=30°, значит АС=2СН=11*2=22 см.
3.
∠В=60°, значит ∠А=90-60=30°, т.к. сумма острых углов прямоугольного треугольника составляет 90°, значит,
АВ=2 ВС
Пусть АВ=х см, тогда ВС=1/2 х см. Составим уравнение:
х+1/2 х=15; 1,5х=15; х=10; АВ=10 см