Ответ:
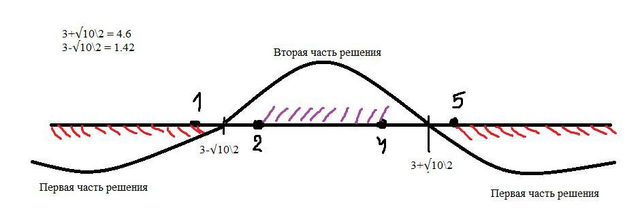
(-∞;1] ∪[5;+∞)∪ [2;4].
Объяснение:
Т.к. это модуль, то его нужно раскрыть. При выражении, которое стоит под модулем больше нуля раскрываем первым способом, а когда то, что стоит под модулем меньше нуля, раскрываем вторым способом:
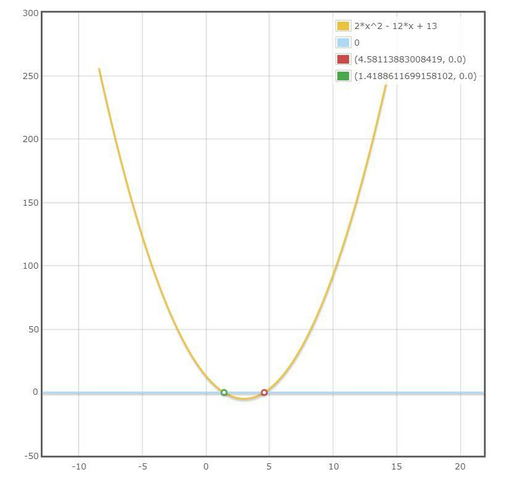
Начертим график выражения, что стоит под модулем (фото 2)
Корнями данного выражения являются значения 
3± 
. Следовательно на промежутке (-∞;3-
]∪ [3
; ∞+) - первая часть решения, а на промежутке между ними - вторая часть.
Первая часть:
Решается оно методом интервалов
2x² - 12x +10≥0
Разделим на 2.
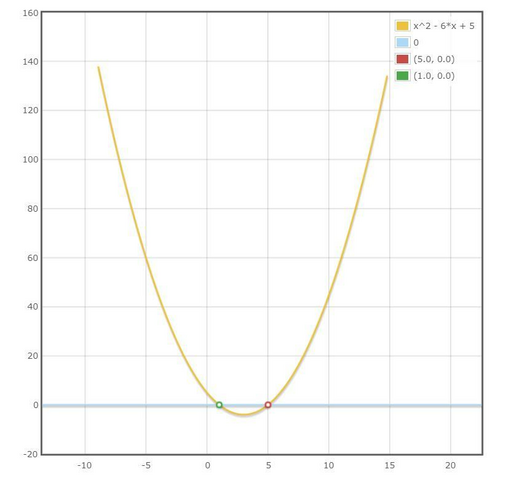
x² - 6x +5≥0
(x-1)(x-5)≥0
Отмечаем точки равные 0 на графике (это точки пересечения с координатной прямой). т.к. у нас больше нуля, то берем части, которые лежат выше прямой. Это:
(-∞;1] ∪[5;+∞). Это и есть ответ.
Примечание. Так же, можно не строить график. Можно отметить точки на прямой, определить знак этих интервалов, подставив точку вместо х и взять необходимые знаки.
Вторая часть:
Решу ее кратко, но решается она аналогично первой
-2x² + 12x -13≥3
2x² - 12x +16≤0
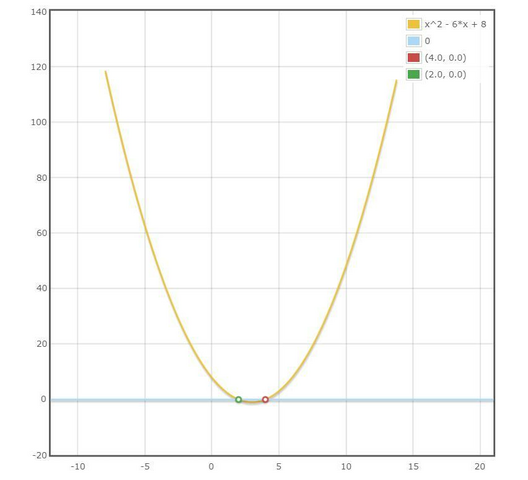
x² - 6x +8≤0
(x-2)(x-4)≤0
см. фото 3 Ответ: [2;4].
НАКОНЕЦ, объединяем оба решения и первоначальный интервал фото 4
