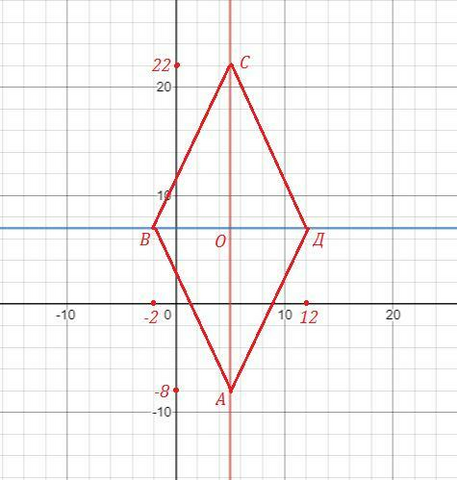
Ответ: Д(12;7) , С(5;22) .
Объяснение:
Соседние вершины А(5;-8) и В(-2;7) .
Осями симметрии ромба являются его диагонали, которые пересекаются под прямым углом. Диагонали заданного ромба пересекаются в точке O(5;7) .
Длина половины диагонали ВД равна ВО=5-(-2)=7 . Точка Д находится на диагонали ВД на том же расстоянии от точки О, что и точка В, то есть ОД=7, тогда координаты точки Д( 5+7 ; 7 ) или Д( 12 ; 7 ) .
Аналогично, АО=1/2*АС , АО=7-(-8)=15 ⇒ ОС=15 .
Точка С( 5 ; 7+15 ) , С( 5 ; 22 ) .