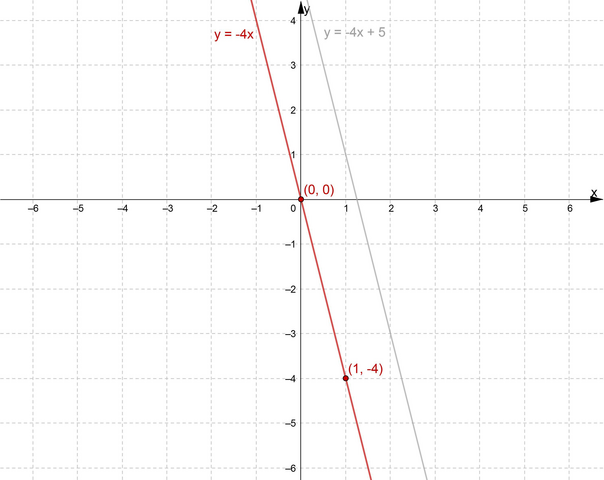
Задача: Задать формулой линейную функцию, график которой параллелен прямой y = −4x+5 и проходит через начало координат. Построить график полученной функции.
Решение:
Т.к. искомая линейная функция параллельна заданной, ее угловой коэффициент будет таким же (k = −4). Линейная функция, проходящая через начало координат (0; 0) — прямая пропорциональность — имеет вид y=kx (b=0).
Следовательно, наша функция будет задана формулой:
y = −4x
Таблица с координатами точек:
x | 0 | 1
y | 0 | −4
Ответ: y = −4x, (график прикреплен).
Задача: График функции y = (3−a)x−a+15 проходит через точку А(−7; 0). Найти значение а.
Решение:
Упростим функцию и подставим координаты точек в полученное выражение:
y = 3x−ax−a+15
0 = 3·(−7)−(−7а)−а+15
0 = −21+7а−а+15
6а = 6
а = 1
Ответ: а = 1.