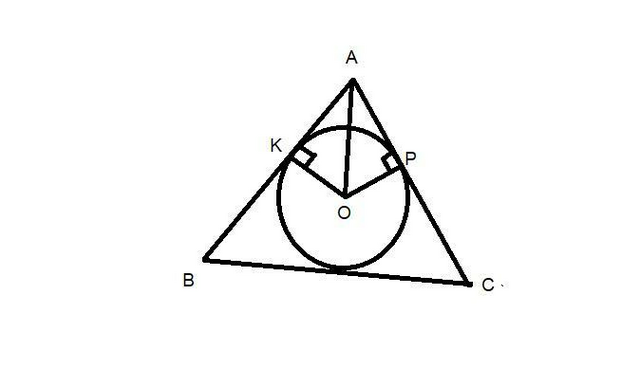
Прямоугольные треугольники равны по гипотенузе и катету
OK=OP=R
OA-общая, значит равная
AK⊥OK и AP⊥OP так как касательные перпендикулярны радиусу вписанной окружности
Из равенства треугольников следует равенство соответствующих катетов AK=AP в этих треугольниках