1) Точка пересечения серединных перпендикуляров (O) равноудалена от вершин.
OM=ON=OK=12
△NOK - равнобедренный, углы при основании равны
NOK =180-30*2 =120
S(NOK) =1/2 ON*OK sin(NOK) =1/2 *12*12 *√3/2 =36√3
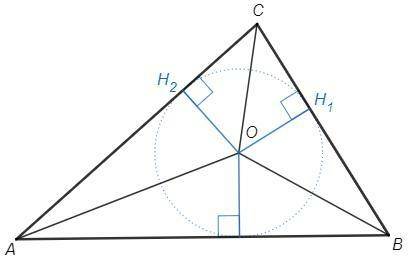
2) Точка пересечения биссектрис (O) равноудалена от сторон. Расстояние (длина перпендикуляра) от вершины до основания - высота. Высоты треугольников AOC и BOC равны, площади относятся как основания.
OH1=OH2
S(AOC)/S(BOS) =1/2 AC*OH2 /1/2 BC*OH1 =AC/BC =8/6 =4/3