Основание пирамиды — правильный треугольник с площадью √3 см2. Две боковые грани пирамиды...

Question

Основание пирамиды — правильный треугольник с площадью √3 см2. Две боковые грани пирамиды перпендикулярны к плоскости основания, а третья — наклонена к ней под углом 30°. а) Найдите длины боковых ребер пирамиды.б) Найдите площадь боковой поверхности пирамиды.​

Answer 1

Sосн=√3 см²

α=30°

найти

SA,SB,SC,

Sб.п - ?

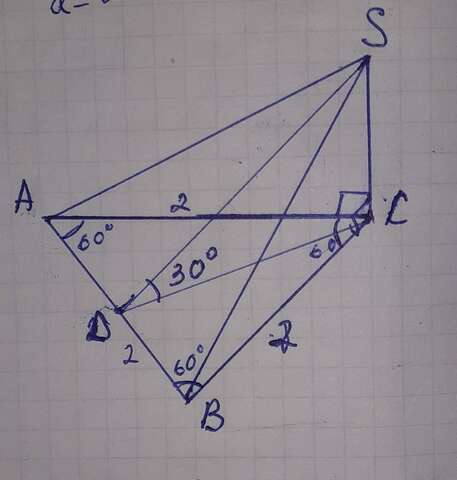
на основании пирамиды SABC правильный равносторонний треугольник ABC. AB=BC=AC=a

формула площади р.т

Sосн =а² ×√3 /4 отсюда сторона треугольника

а=√Sосн×4/√3=√ (4×√3)/√3=√4=2см

грань SAB наклонена к основанию ABC под углом,

двухгранный угол α=30°

находим высоту треугольника ABC на основании

H=CD=а×√3/2=2×√3/2=√3 см

высота треугольника SAB

SD=CD/cosα=√3/cos30°=√3÷√3/2=√3×2/√3=2см

высота пирамиды

SC=SD×sinα=2×sin(30°)=2×1/2=1 cм

длины рёбер SA=SB

SA=√BC²+SC²=√2²+1²=√4+1=√5 см

площадь грани SAB

S1=1/2×AB×SD=1/2×2×2=2см²

площадь грани SBC

S2=1/2×BC×SC=1/2×2×1=1 см²

грани SBC и SAC равны

площадь боковой поверхности пирамиды SABC,

Sб.п= S1+2×S2=2+2×1=4 см²

---

Comments

Спасибо огромное!