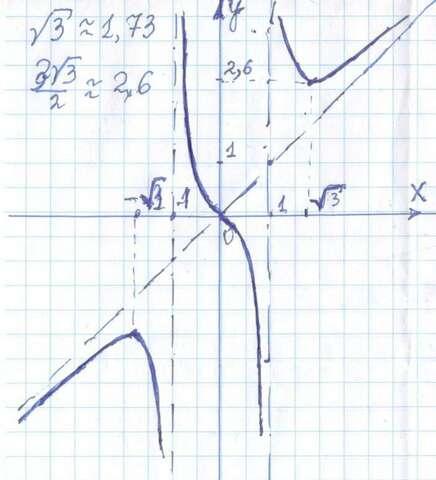
Произвести полное исследование функции f(x) =x³ / (x² - 1) и построить график.
1. ООФ: x ∈ ( -∞ ; -1 ) ∪ ( -1 ; 1) ∪ ( 1 ; ∞). x² - 1 ≠ 0 ; x ≠ ±1 .
вертикальные асимптоты x = -1 и x =1
2. f( -x) = (- x)³ / ( (-x)² -1 ) = - x³ / (x² - 1) = f(x) → нечетная функция
Следовательно , график функции симметричен относительно начала координат (центральная симметрия) , достаточно сначало построить график функции x∈ ( 0 ; ∞) ,а затем дополнить симм. x ( - ∞; 0)
3. Точки пересечения с осями координат
График функции проходит через начало координат: ( 0 ; 0 ) 4. Экстремумы функции
f '(x) = ( 3x²*(x² - 1) - x³*2x ) / (x² - 1)² = x²*(x² - 3) ) / (x² - 1)²
= (x+√3)*x²*(x -√3) ) / (x² - 1)² ||
f '(x) = 0 ⇒x = - √3 ; x=0 , x = √3 → критические (стационарные) точки ,
из них x = - √3 и x = √3 точки экстремумов
+ + + + + + + [- √3] - - - - - - - [0] - - - - - - - [√3] + + + + + + +
x = -√3 _точка максимума ; x = √3 _точка минимума
(точки локальных максимумов и минимумов )
max f(x) = - 3√3 /2 ≈ -2,6 ; min f(x) = 3√3 /2 ≈ 2,6
5. Точки перегиба
f '' (x) = ( f'(x) ) ' = ( x²*(x² - 3) ) / (x² - 1)² ) ' =
( (4x³ -6x)(x² - 1)² -x²*(x² - 3)*2(x² - 1)2x ) / (x² - 1)^4 =
2x ( ( 2x² -3)(x² - 1) -2x²*(x² - 3) ) / (x² - 1)³ =2x(x² +3) / (x² - 1)³
x = 0 точка перегиба
6. Наклонные асимптоты
k = Lim f(x) / x = Lim x³ / x(x² - 1) Lim 1 / (1 - 1/x²) = 1
x→∞
b = Lim( f(x) - k*x ) Lim( f(x) - k*x ) = Lim (x³ / (x² - 1) - 1*x ) =
x→∞
Lim (x / (x² - 1) = 0
x→∞
y = x
- - - - - - - - - - -
P.S. интервалы знакопостоянства функции
f(x) > 0 ; x³ / (x² - 1) > 0⇔ x³ * (x² - 1) > 0 ⇔ (x + 1)x³(x -1) > 0
- - - - - - - ( -1) + + + + + + + (0) - - - - - - - (1) + + + + + + +
f(x) > 0 ⇒ x ∈ ( -1 ; 0) ∪ (1 ; ∞) ;
f(x) < 0 ⇒ x ∈ ( ∞ ;-1 ) ∪ (0 ; 1 ) .
- - -
√3 ≈1,73 ; 3√3/2 ≈ 2,6
график во вложении