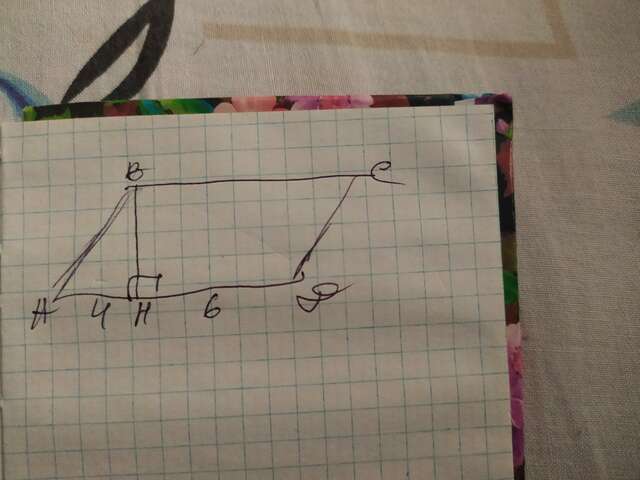Ответ:
Объяснение: 1) диагоналями являются MK и LK
2) второй угол= 70°
3) 6см: (24÷4)=6
4) обозначим эти пропорции как 1х, 5х, 6х, 8х. Зная, что сумма углов четырёхугольника составляет 360°, составляем уравнение:
х+5х+6х+8х=360
20х=360
х=360÷20
х=18. Первый угол=18°. Найдём остальные углы:
18×5=90°
18×6=108°
18×8=144°
Задача:
Обозначим параллелограмм АВСД, а высоту, проведённую к большей стороне- ВН. Рассмотрим получившийся ∆АВН- он прямоугольный. Зная, что ВН делит сторону АД на отрезки 4см и 6см, то сторона АН=4. МЫ знаем, что по условиям, острый угол параллелограмма = 60°, таковым является угол А. Так как ∆АВН прямоугольный, то угол АВН=30°. По свойствам угла 30°(катет, лежащий против этого угла=половине гипотенузы), то гипотенуза АВ=4×2=8см
Итак: сторона АВ=СД=8(см),
АН+НД=4+6=10(см)
Теперь найдём периметр:
P=2×8+2×10=16+20=36(см)