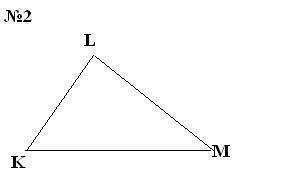
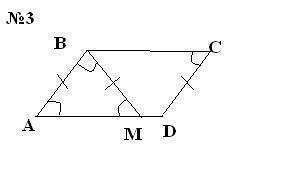
1. Найдите площадь ромба, один из углов которого равен 120 градусам, а сторона 10 см. 2. В треугольнике KLM, KL=2, LM=3, KM=4. Найдите cos K. 3. Периметр параллелограмма ABCD равен 40. Биссектриса угла ABC пересекает сторону AD в точке M. Найдите периметр BMDC, если угол BAD равен 60 градусам, а сторона AB = 8.