Помогите пожалуйста!!! Последний вопрос остался. С помощью циркуля и линейки постройте...

Question

Помогите пожалуйста!!! Последний вопрос остался. С помощью циркуля и линейки постройте равнобедренный треугольник по основанию a и биссектрисе b, проведённой к основанию. Решение проведите в 4 этапа: Этап 1: используя свойства равнобедренного треугольника, проведите анализ задачи. Определите, какие простейшие построения вам понадобятся. Этап 2: выполните построение. Этап 3: докажите, что полученный треугольник – равнобедренный, с длиной основания a и длиной биссектрисы b. Этап 4: исследуйте, сколько решений имеет задача. Всегда ли она будет иметь решения при различных значениях a и b?

Answer 1

1 этап:

Точка, прямая, окружность.

2 этап:

1. На плоскости нужно отметить произвольную точку

2. Через эту точку провести прямую произвольной длины

3. Взять циркуль и провести окружность с центром в точке, которую мы построили в 1 пункте

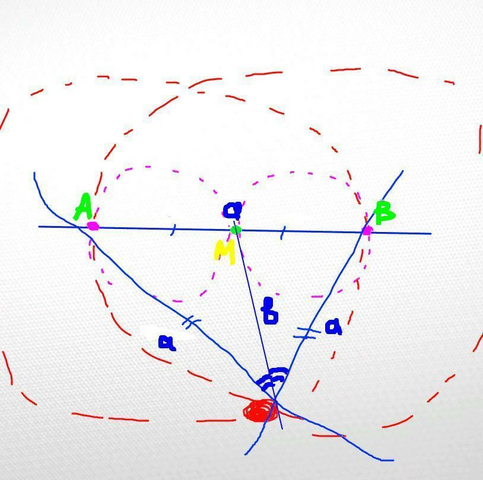
4. Отметить точки пересечения нашей окружности из 3 пункта и прямой (точки А и B) - это будут крайние точки нашего основания.

5. Не изменяя раствора циркуля провести из точек А и B окружности, точка пересечения этих окружностей будет 3 вершиной равнобедренного треугольника.

6. Соединить 3 полученные точки.

3 этап:

Пусть AB = a.

Отметим на нашем основании точку М = b ⋂ a. По рисунку эта точка совпадает с точкой пересечения окружностей, которые мы провели из крайних точек основания: точек А и B.

АМ = BM (как радиусы равных окружностей), а значит т.М совпадает с точкой пересечения медианы и основания. Отсюда, так как медиана совпадает с биссектрисой треугольник является равнобедренным.

4 этап:

Да, всегда будет иметь решения.

---