znanija.com/task/36640973
В ΔABC известен угол A и сторона лежащая против угла А, то есть сторона a. Составить уравнение для нахождения площади ΔABC .
Вычислить площадь данного треугольника
Ответ: S = 0,5a²* (sinβ/sinα )*sin(α+β) .
Пошаговое объяснение :
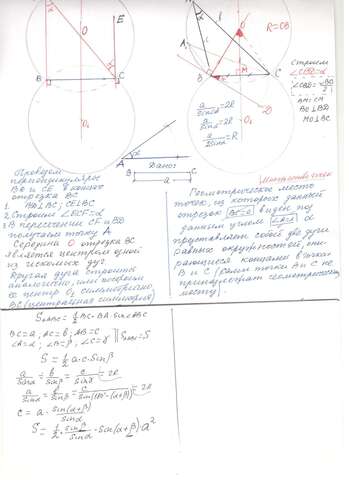
Угол A и сторона лежащая против угла А не фиксирует треугольник ( недостаточно для построения конкретного ||определенного|| треугольника ) см приложение
Нужно добавить еще один элемент, предположим угол B. ||∠B =β ||
∠A =α ; ∠B =β ; ∠C =γ
BC =a ; AC =b ; AB = c
- - - - - - -
S =S(ΔABC) = (1/2)a*b*sin∠C
a/sinα = b/ sinβ = c /sinγ = 2R , где R радиус окружности описанной около треугольника.
* * ∠C=180°-(∠A+∠B) =180°-(α+β)⇒sin∠C=sin( 180°-(α+β))=sin(α+β) * *
a/sinα = b/ sinβ = c/sin(α+β) R= a/2sinα
a/sinα = b/ sinβ ⇒ b= asinβ / sinα
S = (1/2)a*b*sin∠C = 0,5( a*asinβ/sinα )*sin(α+β)
S = 0,5a²(sinβ/sinα)*sin(α+β).