Ответ:
Объяснение: задание 1
Рассмотрим ∆АВД. В нём угол АДВ=90° и угол АВД=45°. Так как этот треугольник прямоугольный, то сумма острых углов составляет 90°, значит угол А= 90-45=45°, следовательно он равнобедренный. В равнобедренном прямоугольном треугольнике катет равен гипотенузе, делённой на √2. Так как в равнобедренном треугольнике углы при основании и стороны равны, то АД=ВД=5√2/√2=5см; АД=ВД=5см
Теперь найдём по теореме Пифагора ВС: ВС=ВД²+СД²
ВС=5²+(√11)²=√(25+11)=√36=6см; ВС=6см
Задание 2
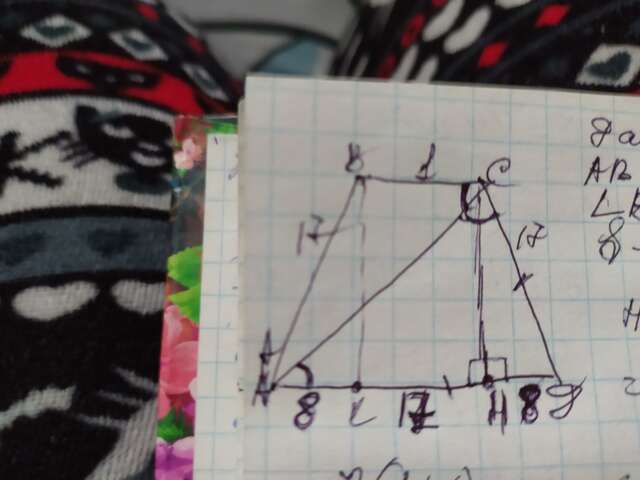
Рассмотрим ∆АСД. По условиям угол АСВ=углу АСД. Также так как АС является секущей при параллельных основах ВС и АД, то угол АСВ=углу САД, как внутренние разносторонние. Углы АСД=углу САД, поэтому ∆АСД- равнобедренный, и СД=АД=17см. Проведём из углов В и С высоты к основанию АД, обозначим их СН и ВК. Они отсекают в середине АД отрезок, равный величине верхнего основания 1см. АК и НД равны и мы можем найти каждый из них: (17-1)÷2=16÷2=8. Итак: АК= НД=8см. Теперь рассмотрим полученный ∆СНД. Он прямоугольный с гипотенузой 17см и катетом 8см. Теперь найдём катет СН по теореме Пифагора: СН=√(СД²-НД²)
СН=17²-8²=√(289-64)=√225=15см
Теперь найдём площадь трапеции зная её высоту СН по формуле:
S=(ВС+АД)/2×СН
S=(1+17)÷2×15=18÷2×15=9×15=135см²
S=135см²