Объяснение:
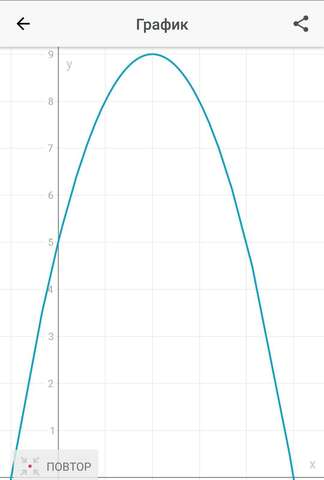
1)y = - x^2 + 4x + 5 - парабола
Если брать общий вид квадратного уравнения y=ax^2+bx+с, то можно увидеть, что в данном случае а<0, значит ветки параболы направлены вниз </p>
y = - (x^2-4x-5)
y= -(x^2-4x-5 +9-9)
y= -(x-2)^2-9, значит вершина будет в точке (2, 9)
-X^2 +4x+5=0
Х^2-4х-5=0
D= 16 + 20 =36=6^2
X1,2= 4±6/2
X1 = 5 X2= - 1, значит на веси абсцыс (весь х) график проходит через точки (-1, 0) (5, 0)
2) Это уже можно увидеть и по графику функции, но если надо расписать, то вот так:
-x^2+4x+5<0</p>
x^2-4x-5<0 </p>
Корни уравнения мы нашли выше: - 1, 5
Рисуем прямую и на ней условно обозначаем корни
---------------------------->х
- 1 5
Теперь возьмём чисто любое число на промежутке, к примеру 0, и подставим в данное уравнение
0^2+4×0+5=5 - значение положительное, значит при любых значениях Х на промежутке от - 1 до 5 значение функции будет положительное
Теперь к примеру возьмем - 2
-(-2)^2+4×(-2)+5= -4-8+5= -7 - значение отрицательное, значит при всех значениях Х на промежутке от минус бесконечности до - 1 значения функции будут отрицательными
Теперь возьмем 6
-6^2 + 4×6+5= - 36+24+5= - 7 - значение отрицательное, значит при всех значениях Х на промежутке от 5 до бесконечности значения функции будут отрицательными
В итоге, значения функции буду отрицательными при значении агумента (-∞, - 1) ∪ (5, +∞)
3) по графику функции видим, что функция возростает при х(-1, 2)