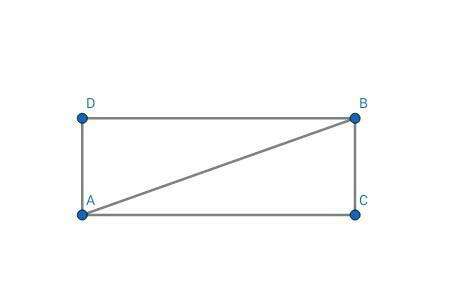
1.Решение.
∠1 = ∠2, по условию (они накрест лежащие углы, а если накрест лежащие углы равны, то прямые параллельны, но в данной задаче эти сведения не важны)
АВ - общая сторона.
=> Эти треугольники равны, по гипотенузе и острому углу.
Ч.Т.Д.
2.Решение.
Сумма смежных углов равна 180°
Внешний угол при вершине В смежный с ∠В => ∠В = 180 - 120 = 60°
Сумма острых углов прямоугольного треугольника равна 90°
=> ∠А = 90 - 60 = 30°
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> АВ = 4 × 2 = 8 см.
Ответ: 8 см.
3.Решение.
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> АС = 12 ÷ 2 = 6 см.
Ответ: 6 см.
4.Решение.
Пусть x - ∠1, тогда х - 46 - ∠2
Сумма острых углов прямоугольного треугольника равна 90°
х + (х - 46) = 90
2х = 136
х = 68
68° - ∠1
∠2 = 68 - 46 = 22°
Ответ: 22°; 68°
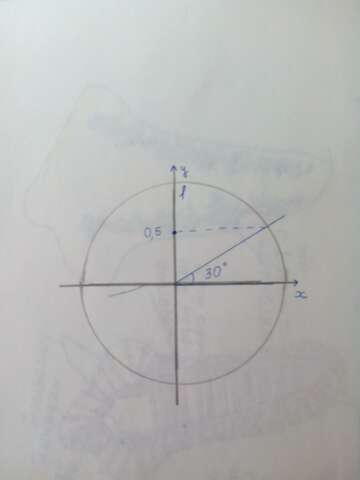
5.На рисунке.